നഷ്ടപ്പെട്ടവ തേടുമ്പോൾ STATISTICS സഹായമാകുന്നത് എങ്ങനെ ?

2011-ൽ രണ്ട് വർഷമായി കാണാതായ ഒരു എയർ ഫ്രാൻസ് വിമാനം കണ്ടെത്താൻ സ്റ്റാറ്റിസ്റ്റിക്‌സാണ് സഹായിച്ചത്.

 
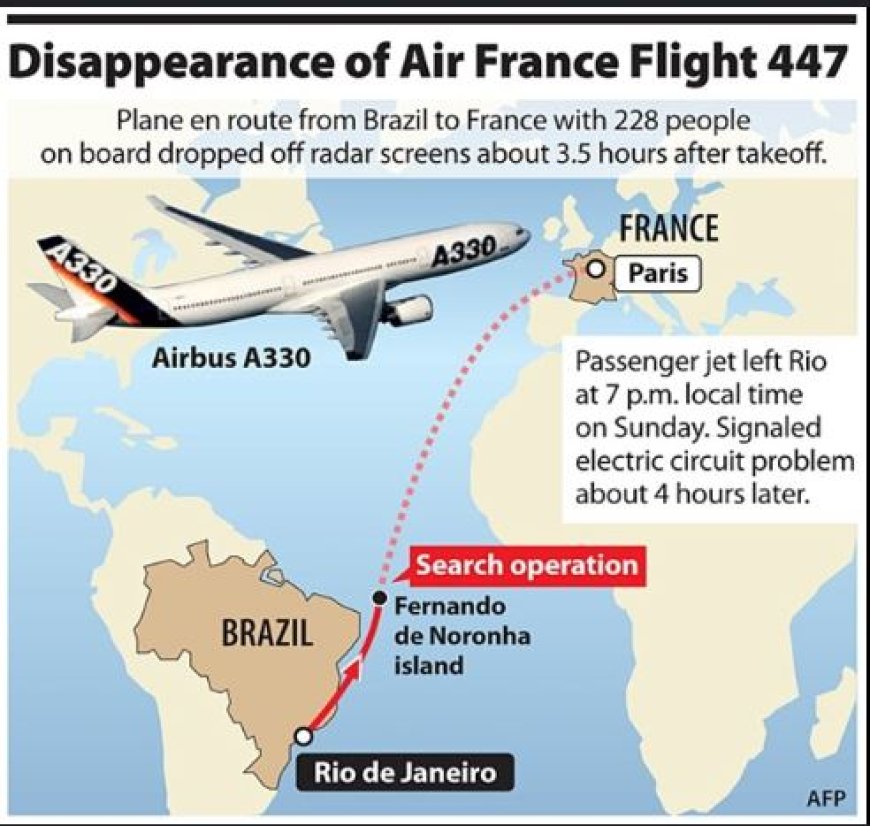
2009 ജൂണിൽ, ബ്രസീലിലെ റിയോ ഡി ജനീറോയിൽ നിന്ന് ഫ്രാൻസിലെ പാരീസിലേക്ക് പറന്നുകൊണ്ടിരുന്ന എയർ ഫ്രാൻസ് ഫ്ലൈറ്റ് 447 പെട്ടെന്ന് അപ്രത്യക്ഷമായി. എയർബസ് A330 ൻ്റെ  അവശിഷ്ടങ്ങൾ അഞ്ച് ദിവസത്തിന് ശേഷം അറ്റ്ലാന്റിക് സമുദ്രത്തിൻ്റെ ഉപരിതലത്തിൽ പൊങ്ങിക്കിടക്കുന്നതായി കണ്ടെത്തി, പക്ഷേ വിമാനം തകർന്നതിൻ്റെ രഹസ്യമറിയണമെങ്കിൽ ബ്ലാക്ക് ബോക്സും കോക്ക്പിറ്റ് വോയ്‌സ് റെക്കോർഡറും കണ്ടെത്തേണ്ടതുണ്ട് .

വിമാനത്തിൻ്റെ കുറച്ച് അവശിഷ്ടങ്ങൾ കണ്ടെത്തിയാൽ വിമാനത്തിൻ്റെ ബാക്കി ഭാഗം കണ്ടെത്തുന്നത് എളുപ്പമാകുമെന്ന് നിങ്ങൾ കരുതിയേക്കാം, പക്ഷേ അത് അത്ര ലളിതമല്ല. കുറച്ച് ദിവസങ്ങൾക്ക് ശേഷം, സമുദ്രപ്രവാഹത്തിനൊപ്പം അവശിഷ്ടങ്ങളും ഒഴുകി  നീങ്ങുമായിരുന്നു. പ്രാരംഭ ആഘാതത്തിൽ നിന്ന് അവശിഷ്ടങ്ങൾ എങ്ങനെ സഞ്ചരിച്ചുവെന്ന് സിമുലേറ്റ് ചെയ്യാൻ കഴിയുന്ന സോഫ്റ്റ്‌വെയർ നിലവിലുണ്ട്. ഇത് യുഎസ് കോസ്റ്റ് ഗാർഡ് പതിവായി ഉപയോഗിക്കുന്നതാണ്. എന്നാൽ ഈ സാഹചര്യത്തിൽ, ഭൂമധ്യരേഖയ്ക്കടുത്തുള്ള ഈ പ്രദേശം പ്രവചനാതീതമായ സമുദ്ര പ്രവാഹങ്ങൾക്ക് പേരു കേട്ടതിനാൽ  പ്രത്യേകിച്ച് വർഷത്തിലെ ആ സമയത്ത്    അത് സഹായകരമായില്ല.

അമേരിക്കൻ, ബ്രസീലിയൻ, ഫ്രഞ്ച് കപ്പലുകൾ, വിമാനങ്ങൾ, അന്തർവാഹിനികൾ എന്നിവയെല്ലാം വിമാനത്തിനായി തിരഞ്ഞു, പക്ഷേ അവർക്ക് അത് കണ്ടെത്താനായില്ല. ഈ ഘട്ടത്തിൽ ഫ്രാൻസിൻ്റെ വ്യോമയാന അപകട അന്വേഷണ അതോറിറ്റിയായ ബി.ഇ.എ, കടലിൽ നഷ്ടപ്പെട്ട വസ്തുക്കൾ കണ്ടെത്തുന്നതിൽ വൈദഗ്ധ്യമുള്ള യുഎസിലെ ഒരു കൂട്ടം സ്റ്റാറ്റിസ്റ്റിഷ്യൻമാരുടെ സഹായം തേടി.

നിങ്ങൾ വിചാരിക്കും സ്റ്റാറ്റിഷ്യൻമാർക്ക് ഇതിലെന്ത് കാര്യമെന്ന്....??

സീനിയർ അനലിസ്റ്റ് കോളിൻ കെല്ലർ സഹായിക്കാൻ ഫ്രാൻസിലേക്ക് പറന്നു.

"വിമാനം എന്തുകൊണ്ട് തകർന്നിരിക്കാം എന്നതിനെക്കുറിച്ചുള്ള വ്യത്യസ്ത സിദ്ധാന്തങ്ങൾ കൊണ്ടുവരുന്നതിൽ ഫ്രഞ്ച് ബി.ഇ.എ ഇതിനകം തന്നെ അത്ഭുതകരമായി പ്രവർത്തിച്ചിരുന്നു,"   അവർ പറയുന്നു.
ചരിത്രപരമായ അപകടങ്ങളെക്കുറിച്ചും ഇതിനകം നടത്തിയ തിരച്ചിലുകളുടെ ഫലങ്ങളെക്കുറിച്ചും അവർക്ക് ധാരാളം ഡാറ്റ ഉണ്ടായിരുന്നു. ഈ വിവരങ്ങളെല്ലാം സംഖ്യകളും സാധ്യതകളും ആക്കി മാറ്റാൻ, വിർജീനിയയിലെ മെട്രോൺ ഇൻ‌കോർപ്പറേറ്റഡിലെ കെല്ലറും സംഘവും ബയേസിയൻ സ്ഥിതിവിവരക്കണക്കുകളെ ആശ്രയിച്ചു.

ഇത്തരത്തിലുള്ള ചിന്താഗതി ഒരേ സമയം വിവിധ സാഹചര്യങ്ങൾ വിലയിരുത്താൻ നിങ്ങളെ അനുവദിക്കുന്നു - പരസ്പരവിരുദ്ധമായവ പോലും. ഓരോന്നും ശരിയാകാനുള്ള സാധ്യത ഒരുമിച്ച് കൊണ്ടുവന്ന് ഏറ്റവും സാധ്യതയുള്ള പരിഹാരം നൽകുന്നു. നിങ്ങൾ പുതിയ വിവരങ്ങൾ കണ്ടെത്തിയാൽ, നിങ്ങൾക്ക് നിങ്ങളുടെ മാതൃക എളുപ്പത്തിൽ പരിഷ്കരിക്കാനാകും.

കെല്ലറും സഹപ്രവർത്തകരും ലഭ്യമായ എല്ലാ വിവരങ്ങളും പരിശോധിച്ച് ഓരോ ഡാറ്റയുടെയും അനിശ്ചിതത്വം വിലയിരുത്തി - വിമാനത്തിൻ്റെ  ഏറ്റവും സാധ്യതയുള്ള സ്ഥാനം നിർണ്ണയിക്കാൻ സാധ്യതയുടെ ബയേസിയൻ തത്വങ്ങൾ പ്രയോഗിച്ചു.

സംഘം തിരച്ചിൽ മേഖലയെ ഒരു ഗ്രിഡായി വിഭജിച്ചു, വിമാനം അവിടെ കണ്ടെത്താനുള്ള സാധ്യതയെ പ്രതിനിധീകരിക്കുന്ന ഒരു പ്രൊബേബിലിറ്റി ഓരോ സെല്ലിലും പ്രയോഗിച്ചു. ഈ കണക്കുകൾ കണക്കാക്കാൻ, അവർ ആദ്യം വിമാനം തകരാൻ കാരണമായതിനെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങൾ പരിശോധിച്ചു. ഉദാഹരണത്തിന്, വിവിധ മെക്കാനിക്കൽ തകരാറുകളുടെ സാധ്യത അവർ വിലയിരുത്തി, ഓരോ സാഹചര്യത്തിനും ഒരു സാധ്യത കണ്ടെത്തി.

തുടർന്ന് അവർ മുൻ അപകടങ്ങളിൽ നിന്നുള്ള ചരിത്രപരമായ ഡാറ്റ വിലയിരുത്തി, ഉദാഹരണത്തിന്, വിമാനങ്ങൾ സാധാരണയായി  അവസാനമായി ഉണ്ടായിരുന്നതായി അറിയപ്പെടുന്ന സ്ഥലത്തിന് വളരെ അടുത്തായി കണ്ടെത്തിയിരുന്നുവെന്ന് ചൂണ്ടിക്കാട്ടി. ഒടുവിൽ, കെല്ലറും സംഘവും വിമാനം ഇതിനകം തിരഞ്ഞ സ്ഥലങ്ങളിൽ കണ്ടെത്താനുള്ള സാധ്യത കുറച്ചു കൊണ്ടു വന്നു.

"ബയേസിയൻ ഗണിതശാസ്ത്രത്തിന് രണ്ട് ഘടകങ്ങളുണ്ട്, അത് അതിനെ അദ്വിതീയമാക്കുന്നു. ഒന്നും ഉറപ്പില്ലാത്തതിനാൽ വളരെ പ്രധാനപ്പെട്ട അനിശ്ചിതത്വങ്ങൾ ഉൾപ്പെടെ നിങ്ങളുടെ എല്ലാ ഡാറ്റയും പരിഗണിക്കാൻ ഇത് നിങ്ങളെ അനുവദിക്കുന്നു,"  കെല്ലർ പറയുന്നു.

രണ്ടാമത്തെ നേട്ടം, ബയേസിയൻ സമീപനം വളരെ വഴക്കമുള്ളതാണ് എന്നതാണ്, കെല്ലർ പറയുന്നു.

നിങ്ങളുടെ അറിവ് എപ്പോൾ വേണമെങ്കിലും അപ്‌ഡേറ്റ് ചെയ്യാൻ ഇത് നിങ്ങളെ അനുവദിക്കുന്നു.

പുതിയ എന്തെങ്കിലും വന്നാൽ, നിങ്ങൾ അത് ഫാക്ടർ ചെയ്ത് പ്രോബബിലിറ്റി മാപ്പ് അപ്‌ഡേറ്റ് ചെയ്യുക.
എയർ ഫ്രാൻസ് വിമാനത്തിൻ്റെ കാര്യത്തിൽ, വിമാനം അതിൻ്റെ ഓൺ-ബോർഡ് കമ്പ്യൂട്ടർ സിസ്റ്റം അവസാനമായി സൂചിപ്പിച്ച സ്ഥലത്തിൻ്റെ 40 മൈൽ ചുറ്റളവിൽ തകർന്നുവീണിട്ടുണ്ടെന്ന് അവർക്ക് ഉറപ്പിക്കാമായിരുന്നു. എന്നിരുന്നാലും ഈ പ്രദേശം വളരെ വലുതായതിനാൽ അന്വേഷകർ എവിടെ നോക്കണമെന്ന് അറിയാൻ പാടുപെടുകയായിരുന്നു.

കെല്ലർ നൽകിയ സാധ്യതാ ഭൂപടം, നേരെമറിച്ച്, തിരയാൻ വളരെ ഇടുങ്ങിയ ഒരു പ്രദേശം നൽകി.
ഒരു അപകടത്തിന് ശേഷം, 90% കേസുകളിലും ബ്ലാക്ക് ബോക്സ് ഒരു സിഗ്നൽ പുറപ്പെടുവിക്കുമെന്ന് ചരിത്രപരമായ ഡാറ്റ കാണിച്ചു. അപകടത്തിന് തൊട്ടുപിന്നാലെ, അവസാനമായി അറിയപ്പെടുന്ന സ്ഥലത്തിന് സമീപമുള്ള പ്രദേശങ്ങൾ വൃത്തിയാക്കാൻ തിരച്ചിൽ സംഘങ്ങൾ ധാരാളം സമയം ചെലവഴിച്ചു, ബ്ലാക്ക് ബോക്‌സിൻ്റെയോ വോയ്‌സ് റെക്കോർഡറിൻ്റെയോ പിംഗ് ശ്രദ്ധിച്ചു.

അവർ ഒന്നും കേട്ടില്ല. അതിനാൽ വിമാനം അവിടെ കണ്ടെത്താനുള്ള സാധ്യത വളരെ കുറവാണെന്ന് കെല്ലറും സംഘവും തീരുമാനിച്ചു. എന്നാൽ ബ്ലാക്ക് ബോക്‌സോ വോയ്‌സ് റെക്കോർഡറോ സിഗ്നൽ അയയ്ക്കുന്നില്ലെങ്കിൽ എന്തുചെയ്യും?  മെട്രോൺ സ്റ്റാറ്റിസ്റ്റിഷ്യൻമാർ ഇപ്പോൾ അവരുടെ മാതൃക ഈ സാധ്യമായ സാഹചര്യത്തിന് അനുയോജ്യമാക്കുകയും ഉയർന്ന സാധ്യതയുള്ള ഒരു പുതിയ മേഖല കൊണ്ടുവരികയും ചെയ്തു.
ഒരു സംഘം തിരച്ചിൽ സ്ഥലത്തേക്ക് മടങ്ങി, പക്ഷേ  ഇത്തവണ അവർ വിമാനം കണ്ടെത്തി.
അപകടത്തിൻ്റെ ദുരൂഹത പരിഹരിക്കപ്പെട്ടു.  പൈലറ്റുമാർക്ക് തെറ്റായ സ്പീഡ് റീഡിംഗുകൾ നൽകിയെന്നും അനുചിതമായി പ്രതികരിച്ചുവെന്നും വിമാനത്തിൻ്റെ നിയന്ത്രണം നഷ്ടപ്പെട്ടു എന്നുമാണ്ബ്ലാക്ക് ബോക്സും വോയ്‌സ് റെക്കോർഡർ ഡാറ്റയും സൂചിപ്പിച്ചത് .

"ഞങ്ങൾ അത് കണ്ടെത്തിയത് ഇപ്പോഴും ഒരു ചെറിയ അത്ഭുതമാണ്," കെല്ലർ പറയുന്നു.
"അവശിഷ്ടങ്ങൾ സമുദ്രത്തിൻ്റെ അടിത്തട്ടിൽ, വളരെ മണൽ നിറഞ്ഞ പ്രദേശത്ത് ഉണ്ടായിരുന്നത് ഭാഗ്യമാണ്. ഹിമാലയം പോലെ കാണപ്പെടുന്ന ചില പ്രദേശങ്ങൾ അവിടെ ഉണ്ടായിരുന്നു - പർവതങ്ങൾ, പാറക്കെട്ടുകൾ, താഴ്‌വരകൾ എന്നിവയുടെ കാര്യത്തിൽ." വിമാനം ആ പ്രദേശങ്ങളിലൊന്നിൽ ആയിരുന്നെങ്കിൽ, "അത് എന്നെന്നേക്കുമായി കണ്ടെത്താനാകുമായിരുന്നില്ല" എന്ന് അവർ പറയുന്നു.
ഇങ്ങനെ അപ്രത്യക്ഷമാകുന്ന വിമാനങ്ങൾ, കപ്പലുകൾ എന്നിവ കണ്ടെത്താൻ

 സ്റ്റാറ്റിസ്റ്റിക്സും പ്രൊബേബിലിറ്റിയും നിർണായകമായി  സഹായിക്കുന്നു എന്ന് ആധുനിക ലോകം മനസിലാക്കി .